D.E. Bayleranís Hypotrochoids
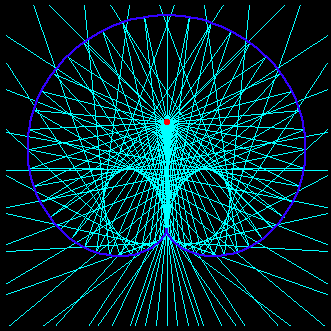
In my study of cycloid curves, I wish to discover new, more accurate forms of graphing as well as perimeter equations for polar figures. I have begun my exploration by examining the limacon. Though Iím not sure if this method has yet been discovered, I have found that a limacon can be graphed by the intersection of congruent circles which pass through the point (1, pi/2) or the point (1, 2pi) depending on wether the limacon is of form r = b + asin(theta) or r = b + acos(theta). I will explain my method with the graph, r = 1 + 2sin(theta).There is first circle with a radius of 1, and its center is located at the point, (1, pi/2). There are 24 other circles, each also with a radius of 1, with their centers located on the first circle. All of the centers are spaced along the circumference of the first circle equally, being pi/12 radians apart. Letís call the circle with the center on (2, pi/2) circle 1 and, moving counter-clockwise, assign the following circles circle 2, circle 3, circle 4, and so on.
The first point on the limacon is located at (3, pi/2), the top of circle 1. The second point is located at the intersection of circle 2 and circle 3. The third point is located at the intersection of circle 3 and circle 5, and the fourth point is located at the intersection or circle 4 and circle 7. In fact, any point on the limacon is the intersection of two circles, n and 2n Ė 1 (disregarding the point (1, pi/2), where all of the 24 circles intersect). Of course, this rule works for any given number of circles, whether there are 9 circles or 144 circles. This chart may clarify this concept.
circle n 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 circle 2n -1 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 Note that the circles in the circle 2n - 1 row go into numbers above 24. This will occur for any number of circles, be it 24 or 672. If the circle number exceeds the number of circles, just subtract the number of circles from the circle number to get the actual circle number. Also, note for limacons of the form r = Cb + Casin(theta) or r = Cb + Cacos(theta), where C is a factorable whole number constant of a and b, all of the circles (including the circle which contains the centers of the other circles) simply have a radius of C. I have found this method of graphing to be very helpful in my study of cycloidal curves.
In trying to discover a substantial method of finding the perimeters of polar curves, I have found a way to express the relation between the circumference of an ellipse and the circumference of a circle with a radius equal to the minor axis of the ellipse. I thought this of a way of finding a "stretch factor," meaning by what factor a circle is stretched to form an ellipse or simply the circumference of an ellipse divided by the cirumference of a cirlce with a radius equal to the minor axis of the ellipse. The stretch factor is just how much the circumference of a circle of radius b is multiplied by to result in a the circumference of an ellipse of major axis a and minor axis b. These strech factors can be found using the ratio of the the major axis of an ellipse to the minor axis of the ellipse. The formula for this is SF = (2 + 2a^2/b^2)^(1/2)/2.